Определение внутренней нормы доходности для оценки привлекательности проекта

Инвестирование – один из интересных способов заработка средств, который заключается в покупке выгодных (по мнению инвестора) активов перспективных компаний и проектов. В мире, который построен на современных рыночных (капиталистических) правилах игры, именно этот процесс является одной из его двигающих сил.

Но как определить, что тот или иной проект действительно выгоден и принесет доход? Стопроцентной гарантии никто никогда дать не может – это обратная сторона медали такого способа заработка. Тем не менее, расчет рисков для той или иной ценной бумаги (или облигации) возможно легко произвести вычисление, что минимизирует вероятность невыгодной покупки.

Именно для этих целей и была создана формула расчета ВНД (англ. IRR – «Internal rate of return»). Она включает в себя ключевые финансовые показатели акции или ценной бумаги и является действительно удобным способом рассчитать убыточность (или доходность).

Оценка рисков таким образом является простой и доступной даже тем, кто не слишком знаком с математическим анализом и экономикой, а полученный коэффициент легко анализируется и читается. Как итог: при знании нюансов и соблюдении ряда правил получаем работающий метод для оценки рисков при инвестировании.

Определение понятия и цели расчета IRR

Внутренняя норма доходности (ВНД или IRR) – ключевой критерий анализа любого доступного для инвестирования проекта. Фактически, эта величина позволяет определить минимальную ставку дисконта, при которой дисконтированные доходы от акции, опциона или ценной бумаги находятся в состоянии равенства с суммой вложения.

Фактически, определение ВНД базируется на уравнении, в котором чистая текущая стоимость (рентабельность) является нулевой. При поиске информации об IRR часто можно наткнуться на схожие термины и его варианты: внутренняя норма доходности, внутренняя ставка доходности, внутренняя ставка отдачи, норма рентабельности или норма возврата инвестиций. Проблемы с адаптацией термина привели даже к ряду сложностей при поиске информации о расчетах.

Уравнение ВНД отражает ту ситуацию, когда инвестиционный проект отдает вложившему в него средства не только инвестиционных средств, но и первоначальных вложений в ценные бумаги. Фактически, в нем рассматривается случай, когда соотношение вложенных средств к доходу является равным. Если финансовые показатели проекта приводят инвестора к каноничному уравнению IRR – это значит, что проект принесет столько же денег, сколько на него было потрачено.

Что можно получить от расчета ВНД? Ответ на вопрос о целесообразности вложений куда-либо. Фактически, уравнение позволяет узнать, какой объем вложенных средств сможет вывести проект «в ноль» и не сделать его убыточным. Подгоняя показатели под каноничную форму уравнения, инвестор может легко сравнить значение необходимого капитала с реально доступным ему и принять решение о вложении или отказе от него.

Подобранная ставка, увеличивающая денежный поток, дает возможность прийти к состоянию равновесия в расчетах. Если полученный таким образом показатель ВНД выше ставки прибыли за вложенные средства – инвестиция может быть произведена. Если ниже – проект однозначно не стоит инвестиций.

Формула расчета инвестиционного проекта

Внутренняя норма доходности рассчитывается по следующей формуле:

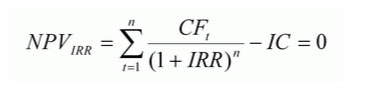
Где:

NPVIRR (Net Present Value)	Чистая текущая стоимость, рассчитанная по ставке IRR.
Cft (от англ. «Cash Flow»)	Размер денежного потока за отрезок времени t.
IC (Invest Capital)	Инвестиционные затраты на проект в первоначальном периоде (тоже являются денежным потоком CF0 = IC).
t	Период времени.

Другой вид формулы (с теми же обозначениями) выглядит так:

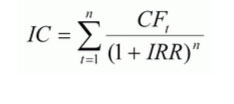
Расчет в Excel

Найти полследовательность арифметических действий, позволяющую вычислять ВНД в Microsoft Office Excel, не представляется возможным. Причина в том, что для полноценного вычисления показателей программой ей придется составить и решить уравнение четвертого порядка – такими функциями данный софт не обладает.

Благо, есть более простой способ: Excel обладает колоссальным запасом встроенных функций, среди которых нашлось место и ВСД (внутренняя ставка доходности). Достаточно лишь пройти в подменю «Финансовые» основной вкладки «Формулы» и выбрать соответствующий пункт в выпадающем списке.

Затем выстраиваем в один из столбцов доходность инвестиции, выделяем их (или прописываем в меню «Значения» при добавлении функции). Результат можно увидеть либо во всплывающем окне (графа «Значение» внизу), либо вывести ее на отдельную ячейку и изменять показатели, просчитывая каждое условие отдельно.

Ответ будет получен при определенных условиях:

• когда в перечне данных имеется хотя бы одно отрицательное число (при отсутствии отрицательного денежного потока IRR даже теоретически не может равняться 0);
• при правильном порядке указания поступлений (сначала первый год (месяц, квартал), потом второй, третий и так далее);
• если не введены данные в поле «Предположение» – это может повлиять на вычисление, производимое методом итераций (подбора).

Графический метод определения ВНД

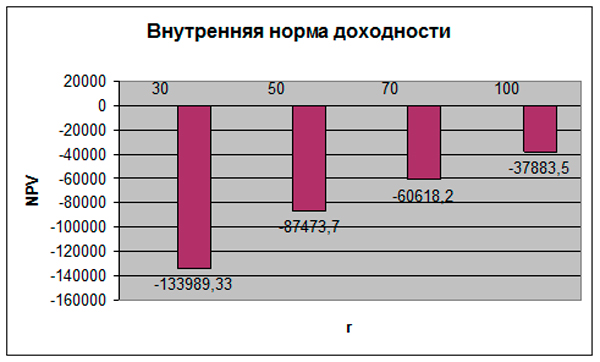
Основное преимущество использования графического метода заключается в наглядности и простоте: достаточно просто построить таблицу и на ее основании (на компьютере или даже вручную) создать график зависимости.

В таблицу необходимо внести периоды, а также данные по денежным потокам проекта (или даже нескольких). Наиболее удобно делать это в том же табличном процессоре Excel. Дисконтировать по разным процентным ставкам (например, 5, 10 и 15%) и затем подобрать показатель более точно можно по приведенному в статье аналитическому алгоритму.

Далее на простроенных графиках ищем нулевую ось (где NPV = 0) и смотрим, какой ставке соответствует проект. Большой плюс метода – возможность наглядно сравнить инвестиционный потенциал сразу нескольких опций одновременно.

Практическое применение коэффициента

Любая инвестиция предполагает расставание с определенной суммой денежных средств, которые в теории должны дать уже прибыль (положительную разницу дохода с расходом). Показатель IRR дает ценную информацию: кредитную ставку, при которой инвестиция не окажется убыточной. При составлении уравнения определяются условия, когда проект не будет ни прибыльным, ни убыточным.

Далее все предельно просто: в случае, если показатель ВНД больше, чем общая итоговая цена капитала – проект стоит рассмотреть для инвестирования. Если нет – он даже теоретически не может быть рентабельным: в таком случае взятые в заем (кредит) средства смогут дать добавочную стоимость при вложении.

Именно по такой схеме и работают банки, проводя операции только с положительным IRR: достаточно сравнить ставки по депозитам (не более 15%) со процентами по выдаваемым в долг деньгам (не менее 20%). Разница же и составит прибыль от деятельности банка (в нашем случае), да и любого инвестиционного проекта в целом. Именно ВНД дает понять, каков максимальный порог возможного займа, который можно вложить в ценные бумаги, компанию и так далее.

Примеры

Пример первый – простейшие практические расчеты при имеющихся базовых показателях. Расчет нормы доходности при неизменной барьерной ставке. Объем вложенных средств равняется 30000$.

Доходы:

Период 1	10000$
Период 2	12000$
Период 3	11000$
Период 4	10500$

Показатель эффективной барьерной ставки — 10%.

Можно произвести вычисления без привлечения софта. Берем стандартный способ подходящего приближения, который часто используется в таких случаях.

Подбираем барьерные ставки приближенно, дабы «окружить» минимальные абсолютные значения NPV, и после осуществляем приближение. Этот метод подразумевает несколько расчетов IRR.

В крайних ситуациях можно построить функцию NPV(r)), но об этом – в разделе ниже.

Произведем вычисления барьерной ставки для r_a=10,0%.

Теперь пересчитаем денежные потоки в виде нынешних стоимостей:

За первый период	PV1 = 10000 / (1 + 0,1)^1 = 9090
За второй период	PV2 = 12000 / (1 + 0,1)^2 = 9917
За третий	PV3 = 11000 / (1 + 0,1)^3 = 8264
За четвертый	PV4 = 10500 / (1 + 0,1)^4 = 7171

Итого, чистая текущая стоимость при ставке 10% (или 0,1) составляет:

NPV = (9090 + 9917 + 8264 + 7171) — 40000 = 4442$.

Теперь попробуем сделать то же, но для ставки в 15%.

Пересчитаем денежные потоки в образ нынешних стоимостей:

• PV₁ = 10000 / (1 + 0,15)^1 = 8695;
• PV₂ = 12000 / (1 + 0,15)^2 = 9073;
• PV₃ = 11000 / (1 + 0,15)^3 = 7232;
• PV₄ = 10500 / (1 + 0,15)^4 = 6003.

Для этой процентной ставки NPV вычисляется аналогично:

NPV = (8685 + 9073 + 7232+6003) — 35000 = — 4007$

Используем формулу приближения и получаем процент:

IRR = r_a + (r_b — r_a) * NPV_a /(NPV_a — NPV_b) = 10 + (15 — 10)*4442 / (4442 — (- 4007)) = 12,6%

Равенство справедливо, если r_a < IRR < r_b и NPV_a > 0 > NPV_b.

Ответ: полученный показатель окупаемости инвестиции составляет 12,6%, что выше заданной вначале эффективной барьерной ставки в 10%. Вывод: проект достоин рассмотрения и может стать рентабельным.

Тем не менее, подобный алгоритм не работает в тех случаях, когда внутреннюю норму доходности необходимо находить при изменяющейся барьерной ставке.

Дано:

Размер инвестиции	$15000
Доходы от инвестирования в проект после одного года	$8000
После второго	$6500
После третьего	$7000
Размер барьерной ставки	12% в первом году
Ставка во втором	11%
В третьем году	10%

Условие то же, что и в прошлом примере: вычислить вероятность окупаемости проекта и целесообразность инвестирования в него. Рассчитаем для ставки дисконтирования одинаковой r_a=20,0%

Пересчитаем денежные потоки в вид текущих стоимостей:

Для первого периода	PV1 = 8000 / (1 + 0,2)^1 = 6666$
Для второго периода	PV2 = 6500 / (1 + 0,2)^2 = 4513$
Для третьего периода	PV3 = 7000 / (1 + 0,2)^3 = 4050$

Подсчитываем внутреннюю норму, как и в предыдущем примере:

NPV = (6666 + 4513 + 4050) — 15000 = 229$

Теперь сделаем те же вычисления для r_b = 25,0%

Пересчитаем денежные потоки в вид текущих стоимостей:

Первый отрезок времени	PV1 = 8000 / (1 + 0,25)^1 = 6400$
Второй отрезок времени	PV2 = 6500 / (1 + 0,25)^2 = 4160$
Третий отрезок времени	PV3 = 7000 / (1 + 0,25)^3 = 3584$

И все та же норма по аналогии:

NPV = (6400 + 4160 + 3584) — 15000 = — 864$

Итоговый показатель составит:

IRR = 20 + (25 — 20)*229 / (229 — (- 864)) = 21%

Так как показатель барьерной ставки изменяется, то сопоставление необходимо сделать именно с показателем внутренней барьерной ставки. В соответствии с расчетом образца эффективная барьерная ставка составит 10,895%. Вывод таков: полученный окупаемости равен 21%, что значительно выше имеющихся средних 11%. Можно смело инвестировать в проект.

Ценное замечание: правило, согласно которому выбирается проект с большим показателем внутренней нормы доходности, действует лишь в общих случаях. Оценка может изменяться кардинально, если учесть реинвестиции. В таком случае показателя барьерной ставки недостаточно проект с меньшим IRR, может быть выгоднее проекта с большими цифрами.

Модифицированная ВНД (MIRR)

Как уже говорилось выше, ВНД учитывает лишь те ситуации, в которых осуществляется первичное инвестирование. В случаях, когда происходит повторное вложение средств, он не работает: полученные по расчетам результаты могут прямо противоречить целесообразности вложения средств. Для облегчения задачи именно в этих ситуациях была создана модифицированная ВНД (или MIRR).

Формула для ее определения выглядит подобным образом, только учитывает ставку реинвестирования:

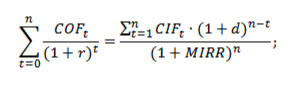
Где:

MIRR	Внутренняя норма доходности инвестиционного проекта.
COFt	Траты на реинвестирование на отрезке времени t.
CIFt	Полученная прибыль.
r	Процентая ставка дисконтирования (или средневзвешенная стоимость активов).
d	Процентная ставка реинвестирования в проект.
n	Количество отрезков времени.

К слову, в Excel имеется и эта функция – она находится в том же списке под названием «МВСД».

Недостатки использование данного метода

Существует ряд существенных недостатков, которые могут оттолкнуть инвестора от использования вычислений на базе IRR:

• относительная громоздкость расчетов в случае большого количества отрезков времени;
• необходимость получения полных и актуальных данных о движении капитала в предприятии – чистая прибыль может отличаться от имеющейся в расчетах;
• графический способ позволяет визуально оценить необходимую величину процентной ставки, но дает лишь приблизительные результаты.

Ограничения и недостатки внутренней нормы доходности

Существует сразу несколько ограничений, которые накладывает на инвестора использование ВНД или МВНД:

• трудно прогнозировать движение денежных средств в будущем – многие факторы формула попросту не учитывает;
• с помощью IRR и MIRR не представляется возможным вычислить дисконтированный объем средств для вложения;
• если брать за основу разные периоды или иметь дело с произвольным чередованием прибыли и убытков – можно получить сразу несколько отличных друг от друга показателей ВНД, что способно запутать при принятии решения;
• стандартная формула ВНД никак не может описать процесс реинвестирования и способна выдавать в этом случае прямо противоречащие реальному положению дел результаты.

ВНД (или IRR) – один из значимых экономических показателей, который подойдет для предварительной оценки потенциала определенного вложения. Метод имеет как преимущества, так и недостатки, но все же среди простых и доступных достоит занять свое заслуженное место. Ключевой плюс – возможность выполнить расчеты четырьмя разными способами (аналитически, графически и посредством табличного процессора).

Среди минусов – весьма скромное количество учитываемых факторов и узкий охват возможных сценариев инвестирования. Также нельзя не отметить большую зависимость от правильности показателей чистой текущей стоимости (NPV).